Oolite Bulletins

Vector angleTo

angleTo

function angleTo(v : vectorExpression) : Number

Returns the angle (in radians) between the target and vectorExpression. This is always a positive value between 0 and π.

I always thought a full circle (360 degrees) was 2*PI , so shouldn't this read :

This is always a positive value between 0 and 2π

Lone_Wolf wrote:

Vector angleTo

angleTo

function angleTo(v : vectorExpression) : Number

Returns the angle (in radians) between the target and vectorExpression. This is always a positive value between 0 and π.

I always thought a full circle (360 degrees) was 2*PI , so shouldn't this read :

This is always a positive value between 0 and 2π

No error here. The angle between two vertors is always between 0 and \pi (180 degrees). Don't know about your knowlodge about vectors, but in short, picture two vectors as arrows originating from a single point. Those vectors define a plane. In that plane those vectors (still originating from that single point) form two angles. The angle between vectors is by definition the smaller of these.

Don't know about your knowledge about vectors

I used to be good at it, did atheneum beta ( pre-requisite for dutch university studies) but that was long ago.

What i'm interested in is a way to determine whether a ship is hit from front side or aft side.

Ok, there are 2 vectors : view direction & direction to attacker.
If the angle is 90 degrees or less, the attacker is in front .

90 degrees = pi / 2 .

It's starting to make sense.

If I follow you correctly, it's the other way around.

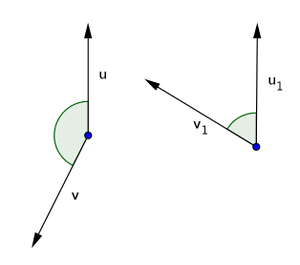
U points to the direction of the player ship and v points to the direction of the attacker. If the attacker is coming from front (the left drawing), the angle is between pi/2 and pi (90 and 180 degrees). And if the attacker is coming from aft (the right drawing), the angle is between 0 and pi/2 (0 and 90 degrees).

A small addendum. If you just want to test if the attacker is coming from front or aft, the dot product is the way to go. It returns negative value when the angle is over 90 degrees and positive when the angle is under 90 degrees.

Spara, i'm used to thinking in coordinate systems, not vectors.

say player ship is at (0,0) , attacker is at (5,5) .

the vector between them has an angle of pi/4 (45 degrees) relative to the positive x-axis.

In short, we look at things a different way and are both right.

I'll look into oolite coordinate system (quaternions i think ?) and associated methods .

Lone_Wolf wrote:

Spara, i'm used to thinking in coordinate systems, not vectors.

For 3D, it's definitely worth the trouble to use vectors. For a game with relative positions and headings even more so. You'll make yourself a big favor by using vectors .

Lone_Wolf wrote:

say player ship is at (0,0) , attacker is at (5,5) .

the vector between them has an angle of pi/4 (45 degrees) relative to the positive x-axis.

Sorry to be pedantic here, but a vector has two properties, magnitude and direction. Depending on the direction of the vector, the angle is different. If the vector is defined from (0,0) to (5,5) then the angle with the positive x-axis will be 45 degrees. If the vector is defined from (5,5) to (0,0) then the angle will be 135 degrees.

Lone_Wolf wrote:

In short, we look at things a different way and are both right.

If we are talking about vectors, then there's only one way to look at things. If you just want to use geometry with lines and angles, that's a different story.

Lone_Wolf wrote:

I'll look into oolite coordinate system (quaternions i think ?) and associated methods .

No need to use quaternions here. Those are used, if you want to do rotations with entities. A plain vector math suffices here.